SSF底物中的氧氣分布

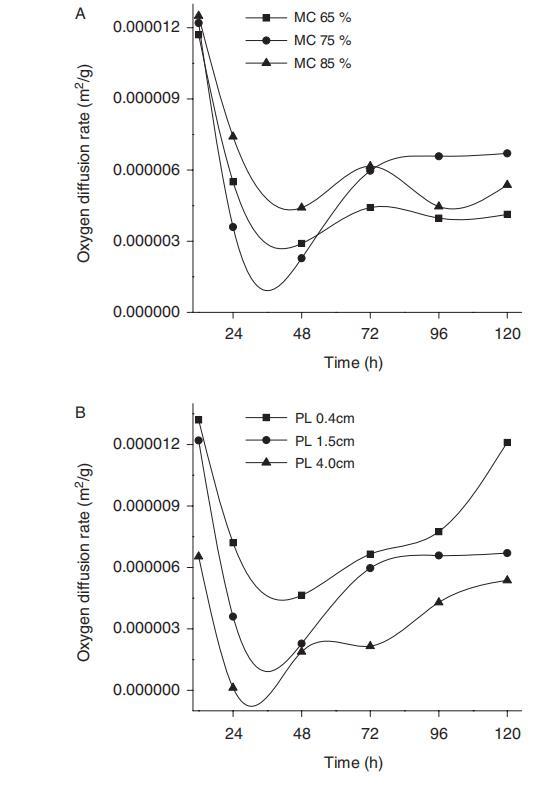
為了研究真菌生長對氧氣擴散的影響，使用微電極測定了固態發酵過程中不同水分含量和顆粒長度的SERS-麩皮底物中的氧氣分布，結果如圖3所示。

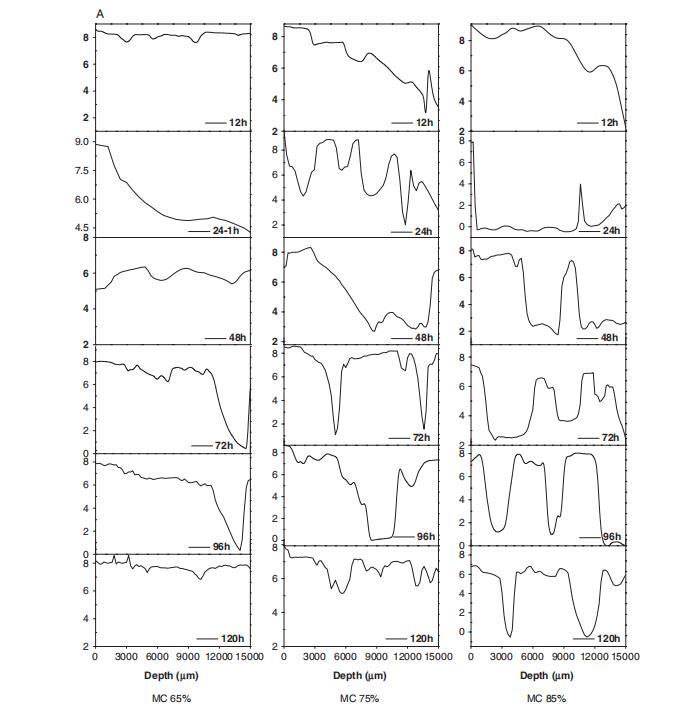
SSF性能與固態底物中的氧氣傳遞密切相關。^19，20在SSF中，由于真菌的生長和氧氣傳遞的限制，固態底物中的氧氣濃度應降低。基于固態底物的孔隙率，在SSF中，真菌生長區域的氧氣濃度應低于沒有真菌的區域。結果表明，在發酵期間，水分含量和顆粒長度實驗中，固態底物中隨深度變化的氧氣濃度分布是不均勻的（圖3）。結果還表明，水分含量和顆粒長度在發酵過程中影響氧氣濃度，這與上述分析一致。在發酵早期（12小時），氧氣濃度的分布幾乎隨著固態底物深度的增加而均勻和連續。然而，在發酵24小時后，它明顯改變。以85%水分含量實驗為例，真菌生物量生長在24小時后促進了固態底物團聚。真菌生物量的密集分布導致固態底物中氧氣濃度降低。這些變化與底物的分形維數變化一致（圖2(A)）。在48小時，隨著真菌在高氧濃度區域的進一步生長，團聚的底物開始分解成小塊，因此孔隙率和分形維數也增加。在72-120小時，固態底物隨著真菌生長進一步分解成更小的團塊；底物孔隙增加導致分形維數增加。結合分形維數，不同水分含量下底物形態的詳細變化表明，隨著水分含量的增加，發酵固態底物的團聚強度增加，并且在發酵48小時后，底物團聚體的分解也更加明顯（圖1(A)和圖2(A)），這與氧氣分布隨發酵進程的變化一致（圖3(A)）。在固態發酵中，真菌菌絲體與固態底物交織形成混合物。同時，底物也相互交織。因此，底物的宏觀結構應通過團聚強度來表達，并且通過宏觀結構的觀察和固態底物相互交織的程度來表達。

顆粒長度也是發酵的重要參數，并且在SSF中明顯影響固態底物的轉化性能。^20研究了顆粒長度對真菌利用SERS生物量以及固態發酵中氧氣分布的影響，結果如圖3(B)所示。結果表明，在4.0 cm顆粒長度下，氧氣濃度的分布比在1.5 cm和0.4 cm顆粒長度下更均勻。同時，在4.0 cm顆粒長度下的團聚強度也低于其他顆粒長度。造成這種情況的主要原因是，4.0 cm顆粒長度底物比其他顆粒長度具有更高的孔隙率，降低了固態底物的粘附強度。0.4 cm和1.5 cm顆粒長度的固態底物更容易團聚，但相應的底物團聚體分解在發酵后期也更明顯。結果還暗示，在0.4 cm顆粒長度下消耗的氧氣比其他顆粒長度多，因為營養物質容易被真菌獲取，從而促進了它們的生長。結果也與分形維數和真菌生物量的分析一致。因此，結果表明，在不同水分含量和顆粒長度的不同固態底物區域中，氧氣分布和變化與固態底物形態變化密切相關，因此可以反映固態發酵中固態底物形態的詳細變化，這也與分形維數一致。

SSF過程中滲透率的計算

底物滲透率變化與其物理結構密切相關，可用于評估固態發酵中的質量傳遞效率。測定了不同水分含量和顆粒長度的固態底物的滲透率，結果如圖4所示。有趣的是，在水分含量和顆粒長度實驗中，滲透率在時間從12小時到48小時內下降，然后隨著發酵時間的增加而增加。滲透率在水含量實驗中遵循65%>75%>85%的順序，在顆粒長度實驗中遵循4.0 cm>1.5 cm>0.4 cm的順序（圖4）。造成這種情況的可能原因是，在固態發酵的初始真菌生長期間，底物孔隙形態導致高滲透率。^18，20隨著發酵過程中真菌的持續生長，固態底物的內部孔隙被菌絲體填充，導致孔隙率降低，從而滲透率降低。這發生在對數生長期和穩定期的早期階段。當真菌生長達到穩定期時，整個固態底物結構因真菌進一步利用底物而受到破壞。小塊底物的增加導致底物孔隙率增加，這導致滲透率增加。在穩定期的后期階段，營養固態底物被真菌進一步利用并降解成更小的碎片，這進一步增加了底物孔隙率，從而增加了滲透率。然而，由于底物重力沉降效應的壓實影響，底物床底部的密度高于底物床頂部的密度，導致相應的低孔隙率底物。因此，在固態發酵48小時后，滲透率的相對增加小于分形維數的增加。

為了進一步證實推斷的合理性以及不同底物特性下真菌生長對底物滲透率的影響，進一步研究了Penicillium decumbens JUA10在不同固態底物中的生長情況，結果如圖4所示。

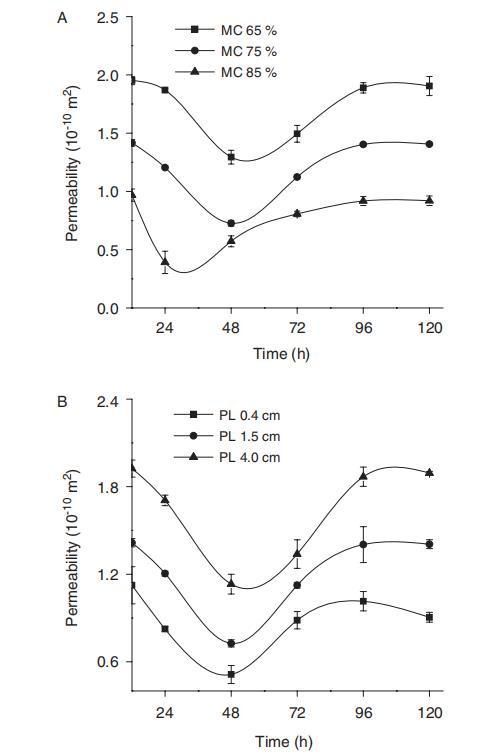
不同條件下真菌生長對固態底物滲透率的影響遵循先前的規則，固態底物滲透率變化應與底物形態的結構變化密切相關。比生長速率符合以下動力學方程：

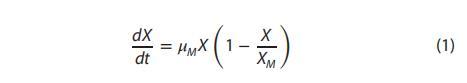
其中K_{m}是發酵過程中空氣滲透率的最小值；K_{M}是發酵過程中空氣滲透率的最大值；mu_{M}是微生物的最大比生長速率；X_{g}是發酵過程中空氣滲透率轉折點對應的生物量；alpha，beta分別是空氣滲透率的比增長速率和比下降速率；k_{1}，k_{2}是與生物量變化相關的等效系數；omega，zeta分別是與菌絲生長相關的空氣滲透率的等效增長速率和等效下降速率。

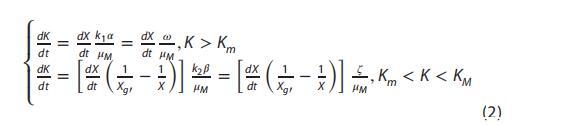
基于上述模型，通過最小偏差法獲得數據。模型參數如表1所示。結果表明，建立的模型可以很好地表達氣體滲透率隨真菌生長的變化。因此，固態底物滲透率的變化與通過分形維數表征的底物形態變化具有相似的趨勢，這與動力學模型一致（圖2和圖4）。然而，有趣的是，滲透率達到最小值的時間比分形維數達到最小值的時間略有滯后（圖2和圖4）。可能的原因是，當真菌菌絲占據大部分固態底物空間時，由于底物本身的重力效應導致的堆積效應不明顯，相應的滲透率無法達到最小值。真菌對固態底物的進一步利用導致小塊產生，這導致底物床高度降低，從而導致最低的空氣滲透率。然而，被真菌降解的固態底物隨后應增加底物滲透率。這一推論也可以通過固態發酵中固態底物中氧氣分布的變化來證實（圖3）。因此，底物滲透率變化也應與底物形態變化密切相關，從而影響質量傳遞效率。

使用分形維數計算氧氣擴散速率

基于固態底物的孔隙率，固態底物的內部結構可以通過曲折度((tau))來量化。^11，14曲折度tau是孔道真實長度與直線長度之比的平方，^12，15反映了多孔介質中孔道的彎曲程度。曲折度((tau))可用于表征通道彎曲程度對固態發酵多孔底物中質量傳遞的影響。^24

傳統的發酵底物中氧氣傳遞系數的測定只能測量宏觀傳遞特性，無法反映孔隙率和底物形態變化對傳遞系數的影響。考慮到固態發酵中不規則孔隙結構和底物形態對氧氣傳遞的影響，使用固態底物的分形維數來表征氧氣擴散速率。根據先前的研究，^25曲折度由分形維數表示如下：

其中，L_{0}是通道的直線距離。在本研究中定義為固態底物高度（15 mm）的線長；lambda是最大通道直徑，可以通過底物顆粒之間的距離計算；D_{B}是底物介質的分形維數。相應的氧氣擴散系數D表示為：^26

D_{0}是宏觀氧氣擴散速率。標準條件下空氣的平均自由程為0.069mu m，這遠小于固態底物的孔徑。因此，在本研究的固態發酵中，空氣擴散是菲克擴散，表示如下：

其中k_{beta}是玻爾茲曼常數，1.3806times 10^{-23}~J~K^{-1};m是氣體的摩爾質量；T是溫度，K;l是分子運動自由程，m;P是壓力，Pa;d是分子直徑，m。三個公式組合表示如下：

氧氣擴散速率可以通過固態底物的多孔結構和分形維數計算，結果如圖5所示。

結果表明，不同底物水分含量和顆粒長度下由真菌生長引起的氧氣擴散速率與分形維數和滲透率的變化趨勢相似，在時間從12小時到24小時期間增加，然后隨著發酵進程而增加。氧氣擴散速率在水含量實驗中幾乎遵循85%>75%>65%的順序，在顆粒長度實驗中遵循0.4 cm>1.5 cm>4.0 cm的順序（圖5）。計算結果與推論結果一致。同時，應該注意的是，氧氣擴散速率不僅是底物的固有特性，而且與真菌代謝引起的底物內部溫度以及固態底物中的氧氣濃度密切相關。因此，結果表明，分形維數應適用于表征固態發酵過程中固態底物中的氧氣傳遞。在使用Penicillium decumbens JUA10對蒸汽爆破稻草進行固態發酵的過程中，氧氣傳遞與底物形態變化密切相關，這可以通過分形維數有效表達。

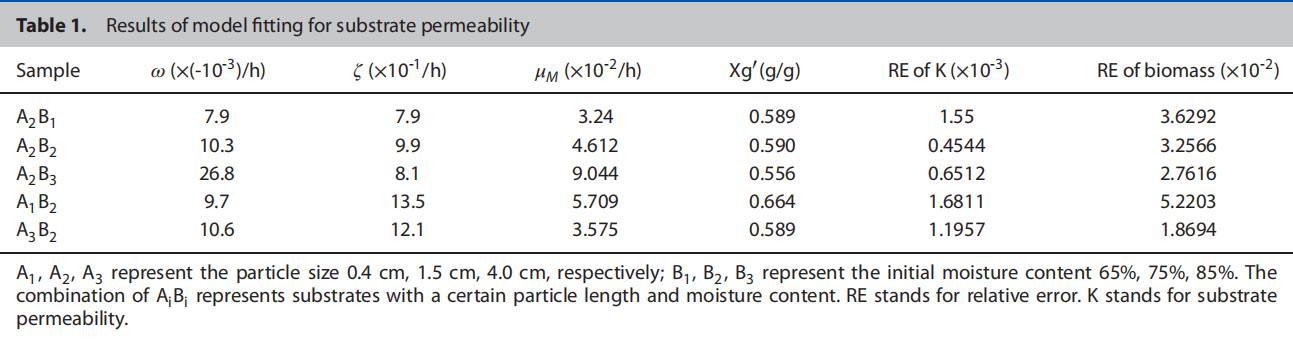
表1.底物滲透率模型擬合結果

結論(CONCLUSIONS)

本研究通過分形維數建立了SSF底物形態與氧氣傳遞之間關系的模型，為表征SSF過程提供了一種更簡便的方法。底物的分形維數能有效表達底物的形態變化、內部氧氣分布和氧氣擴散速率，這與SSF底物的滲透率密切相關。本研究還將SSF底物的一個結構參數引入了氧氣傳遞方程。因此，建立基于SSF過程中底物形態變化的氧氣擴散方程和滲透率模型，應對SSF過程控制和放大具有指導作用。

致謝(ACKNOWLEDGEMENTS)

本工作得到了國家基礎研究計劃（973計劃，項目編號2011CB707401）、國家高技術研究發展計劃（863計劃，2012AA021302）和國家科技支撐計劃重點項目（項目編號2011BAD22B02）的資助。